Как сделать прямоугольный параллелепипед из картона
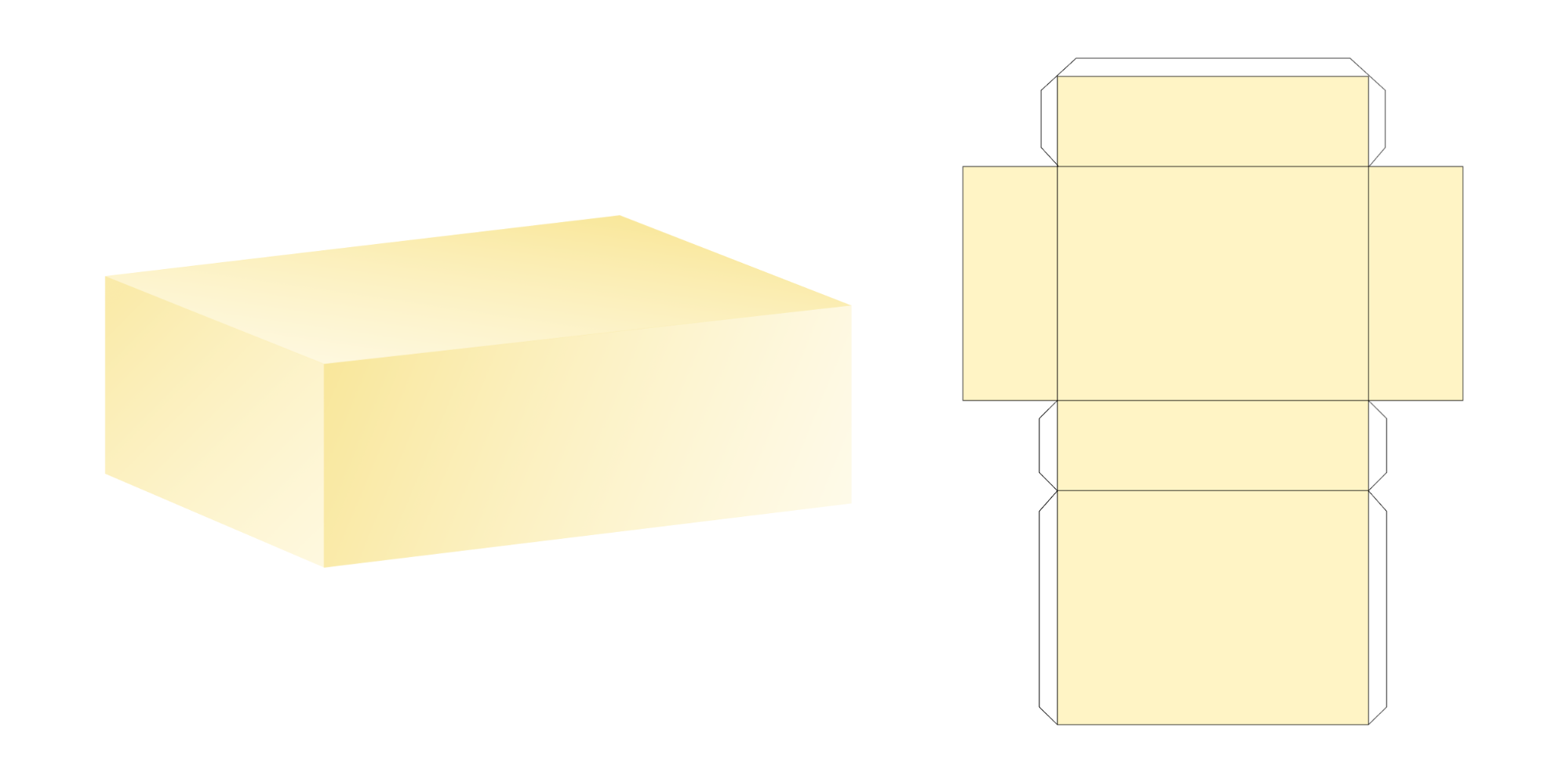
Как сделать параллелепипед из бумаги?
Нна уроке ребята познакомятся с фигурой - прямоугольный параллелепипед. Научатся её делать и изображать в тетради, проверят себя. Урок - изучение геометрического материала на уроках математики.




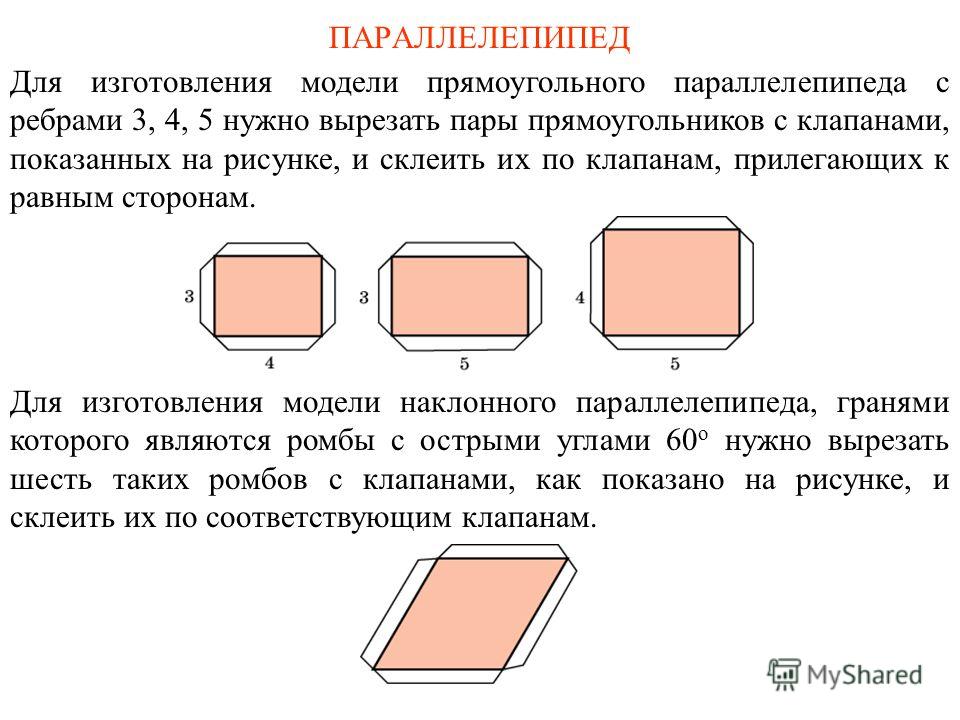





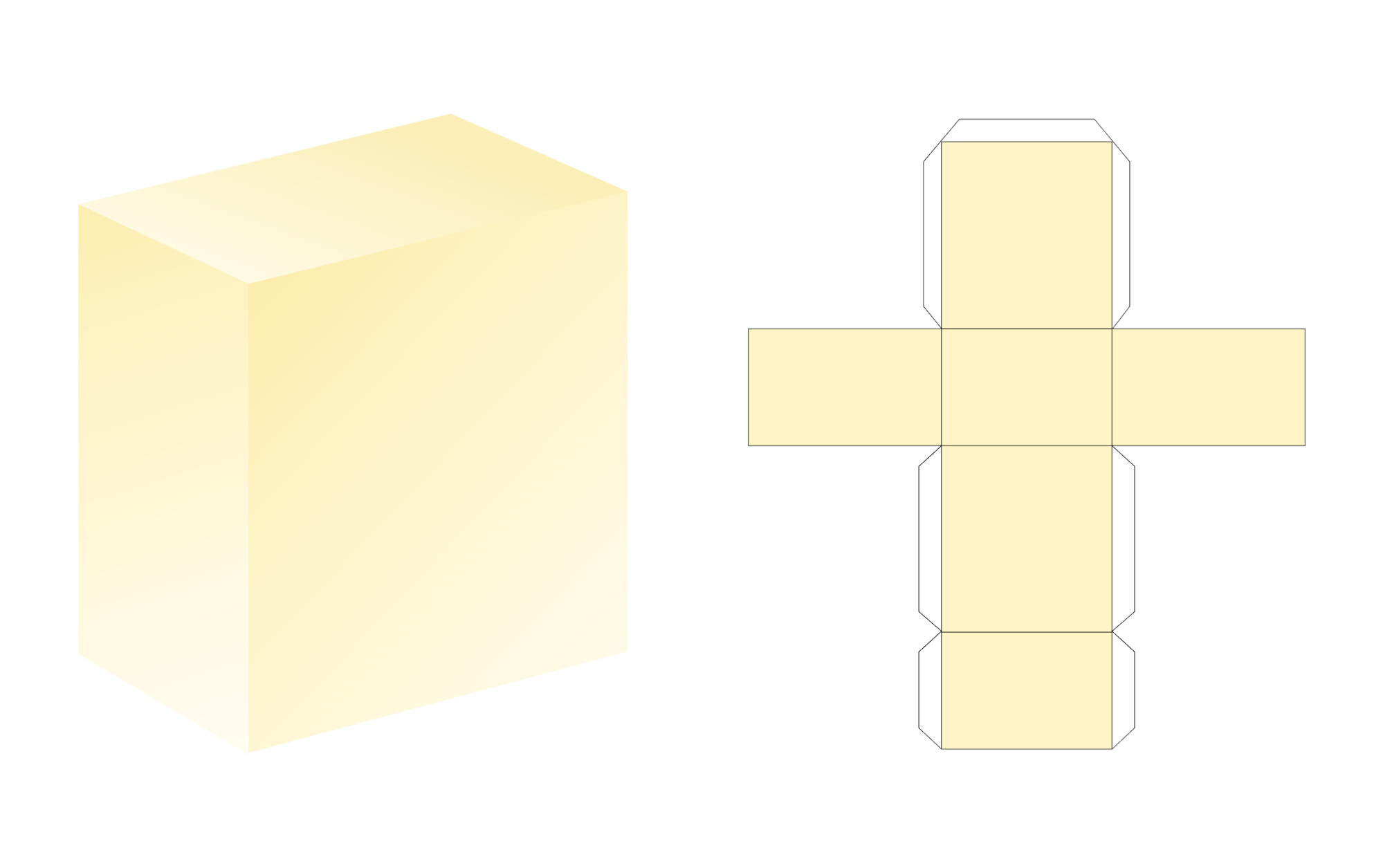


Может оказаться немало причин, когда нужно самому сделать параллелепипед: школьное домашнее задание по выполнению модели простейшего геометрического тела, желание смастерить своими руками упаковку для подарка или даже неповторимое оформление домашнего интерьера. Прямо говоря, все это под силу такой простой форме, как параллелепипед. Из бумаги его сделать проще и быстрее всего.
- Удобная навигация, видео-разборы тем, задачи для самопроверки — всё это в вашем кармане.
- Включите JavaScript для лучшей работы сайта.
- Ученик получит возможность научиться: ясно, точно и грамотно излагать свои мысли; получит возможность для формирования коммуникативной компетентности в общении. Ученик научиться: использовать геометрический язык для описания предметов окружающего мира; осуществлять самоконтроль и взаимоконтроль в процессе достижения результата; осуществлять анализ с целью выделения признаков.
- Прямоугольный параллелепипед — это геометрическое тело со сторонами, которые образуют прямые углы и имеют форму прямоугольника.
- Регистрация Вход. Ответы Mail.
- Играя с ребенком различными геометрическими фигурками, вы помогаете ему развивать пространственное мышление и воображение. Он начинает понимать, что значит квадратный, круглый, кубический, шарообразный, прямоугольный и без труда сможет представить это в своей голове.








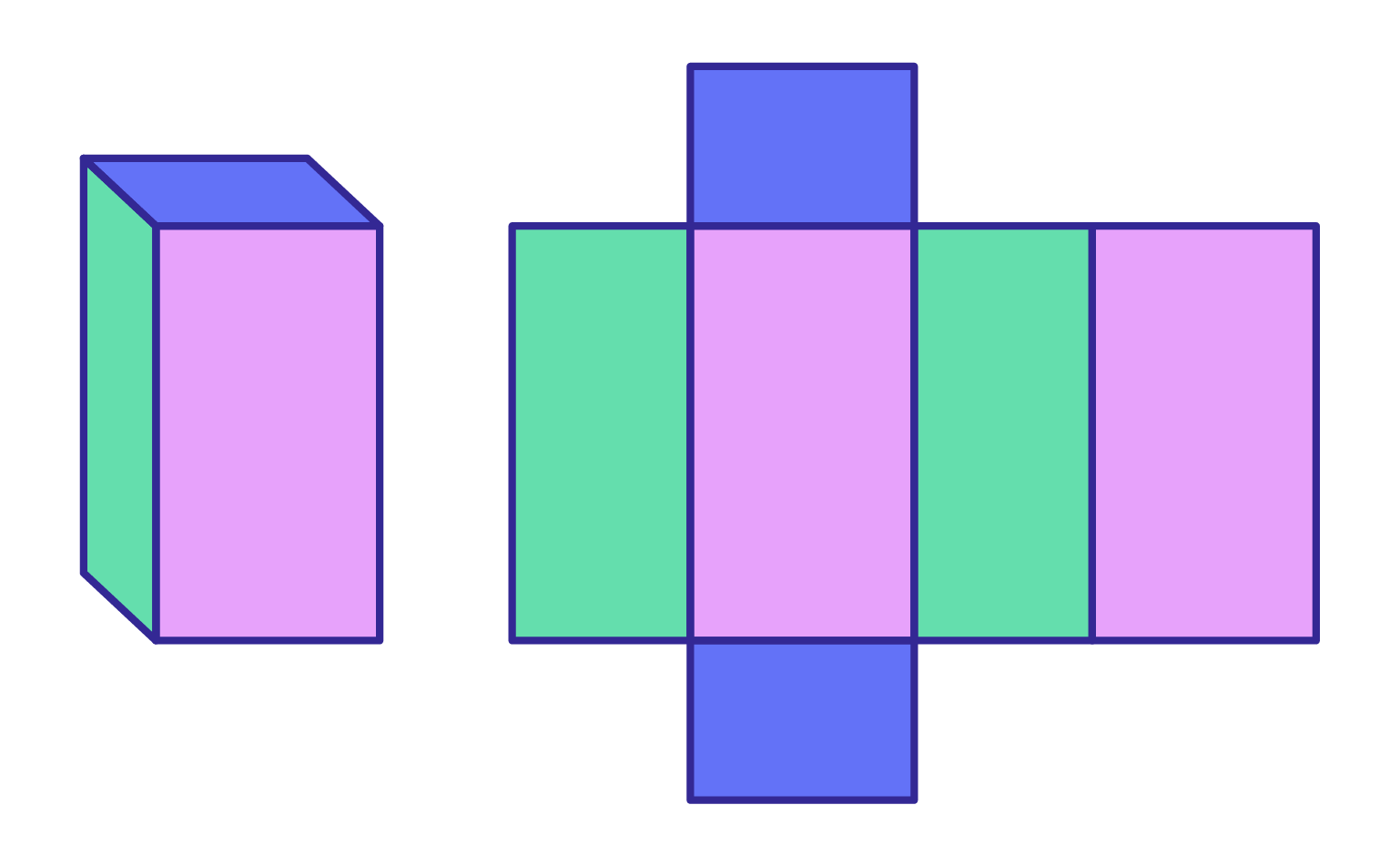





Поверхность куба и прямоугольного параллелепипеда. Площадь треугольника и четырёхугольника. Модели и развёртки. Полная поверхность куба состоит из площадей шести равных между собой квадратов. Значит, для определения полной поверхности куба нужно вычислить сначала площадь одного квадрата одной грани , а потом умножить найденное число на число всех граней, т.